Towards a Clojure Autopilot - Guidance
Now that we have covered the basics , we can move on to the fun stuff, getting from A to B by following a set of GPS coordinates. To actually fly from one way point to another we need two sets of controllers, the ones we defined earlier (roll and pitch hold) will act as our bottom layer on top of that we are going to define another set of controllers (altitude and heading hold) that will modify set points for the bottom layer, i.e altitude hold controls pitch hold to climb or decent to the desired altitude and heading hold controls roll hold to turn the aircraft to the desired heading.
Even though a simple proportional controller worked for the previous example it won't work for the real thing, the reason being that a proportional controller only accounts for the current error so a plane flying against the wind can't accelerate using a proportional controller, it will eventually get stuck at a speed lower than the desired speed. This is where PID controller comes into play, PID stands for Proportional, Integral, Derivative. In a nutshell, proportional term just like before calculates a correction value depending on how far we are away from the desired set point, integral term acts as memory it will respond to accumulated error over time, as accumulated error over time grows integral term will grow which in turn will make our correction grow so even if the wind pushes us back integral term will compensate for it and apply more throttle over time just like a human would, derivative term tries to predict the future by calculating a response to the rate of change of the error basically it makes the controller anticipate approaching the set point.
\begin{equation} correction = K_p \times error + K_d \times (error - prevError) + K_i \times (sumOfErrors) \end{equation}PID formula won't change from application to application, what will change however are those constants (Kp, Kd and Ki). i.e. the more you decrease your Ki constant the less memory your controller will have. Despite the simple looking formula there is an entire theory behind PID so I would suggest googling it for more information on theory and tuning.
(ns autopilot.core (:use clojure.contrib.prxml) (:use clojure.contrib.swing-utils) (:import (javax.swing JFrame JButton) (java.net InetAddress DatagramSocket DatagramPacket))) (def fg-host (InetAddress/getByName "127.0.0.1")) (def fg-port-out 6666) (def fg-port-in 6789) (defn in-thread [f] (doto (Thread. f) (.start))) (defn scale [x in-min in-max out-min out-max] (+ (/ (* (- x in-min) (- out-max out-min)) (- in-max in-min)) out-min)) (defn clamp [x min max] (cond (> x max) max (< x min) min :default x)) (defn pid ([s] (ref (assoc s :integrator 0 :derivator 0))) ([s v] (let [{:keys [set-point kp kd ki integrator derivator bounds]} @s [in-min in-max out-min out-max] bounds v (scale (clamp v in-min in-max) in-min in-max -1.0 1.0) sp (scale (clamp set-point in-min in-max) in-min in-max -1.0 1.0) error (- sp v) p-val (* kp error) d-val (* kd (- error derivator)) integrator (clamp (+ integrator error) -1.0 1.0) i-val (* integrator ki) pid (scale (clamp (+ p-val i-val d-val) -1.0 1.0) -1.0 1.0 out-min out-max)] (dosync (alter s assoc :integrator integrator :derivator error)) pid)))
First we make sure both set point and current value are within the input range, then we map them to a range between -1/+1 so they are a percentage between -100% and 100% of the scale, then we move on with our calculation. The only part that needs special care is the integral part, we need to take care of a problem called integral windup, again think speed, going from 0 to 80 km/h is going to take a long time by the time you reach 80 km/h your integral will be huge and it will make you overshoot the target speed maybe accelerate to 100 km/h then decrease and settle on 80 km/h thats why the integral is kept in range -1/+1. Finally we sum all the terms and scale them to output range.
Moving on to controllers, we have 5 of them,
- Speed Hold
- Heading Hold -> Roll Hold
- Altitude Hold -> Pitch Hold
They all share the same structure a hold function that calculates the correction and a set! function for modifying the set point.
(let [p (pid {:kp 4 :ki 0 :kd 0 :set-point 80 :bounds [0 120 0 1]})] (defn speed-hold [curr] (double (pid p curr)))) (let [p (pid {:kp 2 :ki 1/10 :kd 0 :set-point 0 :bounds [-180 180 -1 1]})] (defn set!-roll [ang] (dosync (alter p assoc :set-point ang))) (defn roll-hold [curr] (double (pid p curr)))) (let [p (pid {:kp 4 :ki 1/5 :kd 0 :set-point 0 :bounds [-90 90 -1 1]})] (defn set!-pitch [ang] (dosync (alter p assoc :set-point ang))) (defn pitch-hold [curr] (* (double (pid p curr)) -1))) (let [p (pid {:kp 15 :ki 1/2 :kd 0.0 :set-point 1000 :bounds [0 10000 -10 10]})] (defn set!-altitude [alt] (dosync (alter p assoc :set-point alt))) (defn altitude-hold [curr] (set!-pitch (int (pid p curr))))) (let [p (pid {:kp 2 :ki 0.0 :kd 0.0 :set-point 90 :bounds [0 180 -10 10]}) norm-ang #(if (and (>= % 180) (<= % 360)) (clamp (scale % 270 360 0 90) 0 90) (clamp (scale % 0 90 90 180) 90 180))] (defn set!-heading [h] (dosync (alter p assoc :set-point (norm-ang h)))) (defn heading-hold [curr] (set!-roll (int (pid p (norm-ang curr))))))
Altitude hold takes the current altitude and calculates a pitch angle for the aircraft that is between -10 and 10 degrees then it changes the set point of the pitch hold to that angle that causes the plane to climb, hold or decent to that altitude.
For navigation, we need to know two things course and distance to target, following two functions are from Aviation Formulary,
(defn bearing [c1 c2] (let [[lat1 lon1] (map #(Math/toRadians %) c1) [lat2 lon2] (map #(Math/toRadians %) c2)] (Math/toDegrees (mod (Math/atan2 (* (Math/sin (- lon2 lon1)) (Math/cos lat2)) (- (* (Math/cos lat1) (Math/sin lat2)) (* (Math/sin lat1) (Math/cos lat2) (Math/cos (- lon2 lon1))))) (* 2 Math/PI))))) (defn distance [c1 c2] (let [[lat1 lon1] (map #(Math/toRadians %) c1) [lat2 lon2] (map #(Math/toRadians %) c2)] (* 2 6371.0 (Math/asin (Math/sqrt (+ (Math/pow (Math/sin (/ (- lat1 lat2) 2)) 2) (* (Math/cos lat1) (Math/cos lat2) (Math/pow (Math/sin (/ (- lon1 lon2) 2)) 2))))))))
bearing returns the heading we need to take to reach c2 from c1, distance returns the distance between points in kilometers.
(let [route (ref [[38.702803 33.454353] [38.756064 33.209744] [38.908678 33.296394]])] (defn dist-to-wp [lat long] (distance [lat long] (first @route))) (defn guidance [heading alt lat long] (when (> alt 400) (let [wp (first @route) dist (distance [lat long] wp)] (set!-heading (bearing [lat long] wp)) (heading-hold heading) (if (and (< dist 1.0) (not (empty? (rest @route)))) (dosync (ref-set route (rest @route))))))))
A simple KML writer for debugging,
(let [path (ref [])] (defn add!-point [long lat] (dosync (alter path conj [long lat]))) (defn dump-log [] (spit "path.kml" (with-out-str (prxml [:decl! {:version "1.0"}] [:kml {:xmlns "http://www.opengis.net/kml/2.2"} [:Document [:name "Flight Path"] [:Style {:id "yellowLineGreenPoly"} [:LineStyle [:color "7f00ffff"] [:width 4]]] [:Placemark [:name "WP-1"] [:Point [:coordinates "33.454353,38.702803"]]] ;;long/lat [:Placemark [:name "WP-2"] [:Point [:coordinates "33.209744,38.756064"]]] [:Placemark [:name "WP-3"] [:Point [:coordinates "33.296394,38.908678"]]] [:Placemark [:name "Path"] [:styleUrl "#yellowLineGreenPoly"] [:LineString [:coordinates (map #(let [[long lat] %] (str long "," lat ", 0.\n")) @path)]]]]])))))
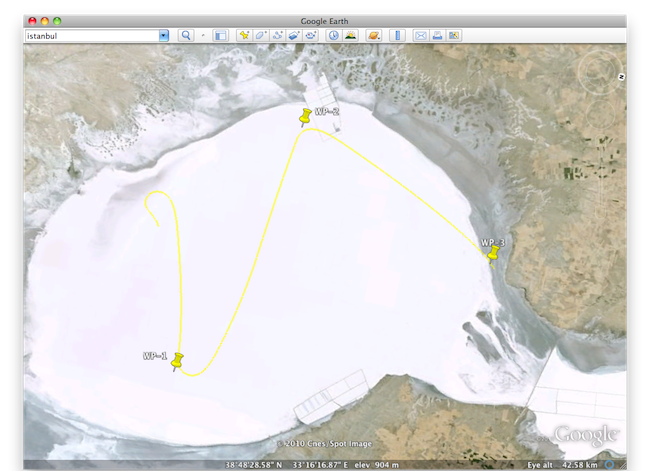
Earth isn't flat so we can't calculate bearing once and be done with it, bearing to way-point will change during the course of the flight so every time guidance is called we calculate a new bearing to the way-point, use it as the set point for the heading hold, heading hold will in turn modify the set point for roll hold just like altitude hold. Once we are within a kilometer of the way point we drop it and move on to the next way-point.
(defn controller [[roll pitch alt heading air-speed lat long]] (add!-point long lat) (altitude-hold alt) (guidance heading alt lat long) (let [roll-cntrl (roll-hold roll) pitch-cntrl (pitch-hold pitch) speed-cntrl (speed-hold air-speed)] (println (format "R %1$.2f %2$.2f" roll roll-cntrl) (format "P %1$.2f %2$.2f" pitch pitch-cntrl) (format "S %1$.2f %2$.2f" air-speed speed-cntrl) (format "A %1$.2f" alt) (format "H %1$.2f" heading) (format "D %1$.2f" (dist-to-wp lat long))) [roll-cntrl pitch-cntrl speed-cntrl])) (defn control-loop [active fn-call] (let [socket-in (DatagramSocket. fg-port-out) buffer-in (byte-array 2048) packet-in (DatagramPacket. buffer-in (count buffer-in)) socket-out (DatagramSocket.)] (in-thread #(try (while @active (.receive socket-in packet-in) (let [state (read-string (String. buffer-in 0 (dec (.getLength packet-in)))) cntrl (fn-call state) msg (str (apply str (interpose \, cntrl)) "\n") buf (.getBytes msg) packet (DatagramPacket. buf (count buf) fg-host fg-port-in)] (.setLength packet-in (count buffer-in)) (.send socket-out packet))) (finally (.close socket-in) (.close socket-out)))))) (defn autopilot [] (let [active (ref false) button (JButton. "Autopilot OFF")] (.setFont button (-> button .getFont (.deriveFont (float 40)))) (add-action-listener button (fn [_] (if (= false @active) (do (.setText button "Autopilot ON") (dosync (ref-set active true)) (control-loop active controller)) (do (.setText button "Autopilot OFF") (dosync (ref-set active false)))))) (doto (JFrame.) (.add button) (.pack) (.setVisible true))))
Before we send a control packet back, we log our current position that way after the flight we can take a look at the path taken in Google Earth, then we let high level controllers calculate new set-points for low level controllers and send calculated correction values from low level controllers to FlightGear.
input-protocol.xml,
<?xml version="1.0"?> <PropertyList> <generic> <input> <line_separator>newline</line_separator> <var_separator>,</var_separator> <chunk> <name>/controls/flight/aileron</name> <node>/controls/flight/aileron</node> <type>float</type> <format>%f</format> </chunk> <chunk> <name>/controls/flight/elevator</name> <node>/controls/flight/elevator</node> <type>float</type> <format>%f</format> </chunk> <chunk> <name>/controls/engines/engine/throttle</name> <node>/controls/engines/engine/throttle</node> <type>float</type> <format>%f</format> </chunk> </input> </generic> </PropertyList>
output-protocol.xml,
<?xml version="1.0"?> <PropertyList> <generic> <output> <line_separator>newline</line_separator> <var_separator>,</var_separator> <chunk> <name>/orientation/roll-deg</name> <node>/orientation/roll-deg</node> <type>float</type> <format>[ %f</format> </chunk> <chunk> <name>/orientation/pitch-deg</name> <node>/orientation/pitch-deg</node> <type>float</type> <format>%f</format> </chunk> <chunk> <name>/position/altitude-agl-ft</name> <node>/position/altitude-agl-ft</node> <type>float</type> <format>%f</format> </chunk> <chunk> <name>/orientation/heading-deg</name> <node>/orientation/heading-deg</node> <type>float</type> <format>%f</format> </chunk> <chunk> <name>/velocities/airspeed-kt</name> <node>/velocities/airspeed-kt</node> <type>float</type> <format>%f</format> </chunk> <chunk> <name>/position/latitude-deg</name> <node>/position/latitude-deg</node> <type>float</type> <format>%f</format> </chunk> <chunk> <name>/position/longitude-deg</name> <node>/position/longitude-deg</node> <type>float</type> <format>%f]</format> </chunk> </output> </generic> </PropertyList>