Fractals in Clojure - Buddhabrot Fractal

Buddhabrot is a special rendering of the Mandelbrot fractal. Rendering technique we will use is developed by Melinda Green.

buddhabrot fractal

First we create a 2D array that will map to the pixel's on the screen. Next we start picking random points on the image and apply the mandelbrot formula. We iterate through the formula for points which do escape within the chosen number of iterations.

To get started we need to get some utility functions out of the way, at first I used the complex number library in clojure-contrib but for some reason they were taking a long time to compute. So I wrote my own. 

(ns buddhabrot
  (:import (javax.swing JFrame JLabel)
           (java.awt Graphics Dimension Color)
           (java.awt.image BufferedImage)))

(defn add
  "Complex addition"
  [c1 c2]
  (map + c1 c2))

(defn multiply
  "Complex Multipication"
  [[real-a imag-a] [real-b imag-b]]
  [(- (* real-a real-b)
      (* imag-a imag-b))

   (+ (* real-a imag-b)
      (* imag-a real-b))])

(defn abs
  "Complex Absulute Value"
  [[real imag]]
  (Math/sqrt 
   (+ (* real real)
      (* imag imag))))

For each point we pick on the screen we need to calculate how the point escapes. 

(defn calc-path
  [x y max-iterations]
  (let  [c [x y]]
    (loop [z c 
           path []
           iterations 0]
      (if (> iterations max-iterations)
        []
        (if (> (abs z) 2.0)
          (conj path z)
          (recur (add c (multiply z z)) (conj path z) (inc iterations)))))))

If the point escapes with in the chosen number of iterations we get a list of points. For each point we get, we increment a counter in the buffer. In the end we color the fractal based on the number of iterations that passed through that pixel.

Since drawing buddhabrot is an expensive operation and takes a long time to render good looking pictures. Calculations are done on a separate thread, generate function will run indefinitely, you can check picture quality using the draw function. Because there will be no output you need to run the script in REPL and call draw to look at it. 

(defn point-to-coordinate [size [real imag]]
  [(int (+ (* 0.3 size (+ real 0.5)) (/ size 2)))
   (int (+ (* 0.3 size imag) (/ size 2)))])

(defn buffer-set [{size :size buffer :buffer} point]
  (let  [[x y] (point-to-coordinate size point)]
    (if (and (> x 0)
             (> y 0)
             (< x size)
             (< y size))
      (aset-int buffer y x (+ 1 (aget buffer y x))))))

(defn generate [fractal]
  (let  [{:keys [buffer iteration]} fractal]
    (doseq [point (iterate inc 1)]
      (let  [x    (- (rand 6) 3)
             y    (- (rand 6) 3)
             path (calc-path x y iteration)]

        (if (= (mod point 1000000) 0)
          (println "Point: " point))

        (doseq [p path] (buffer-set fractal p))))))

(defn start [fractal]
  (future (generate fractal)))

For coloring the image we use the same algorithm that we used to draw the mandelbrot set, 

(defn calc-pixel-color
  [iteration max-iterations]
  (let [gray (int (/ (* iteration 255) max-iterations))
        r    gray
        g    (min (int ( / (* 5 ( * gray gray)) 255)) 255)
        b    (min (int (+ 40 ( / (* 5 (* gray gray)) 255))) 255)]
    (try
      (Color. r g b)
      (catch Exception e (new Color 0 0 0)))))

We iterate through the array paint everything on an BufferedImage then draw that on a JLabel. 

(defn paint-canvas [buffer size graphics]
  (let  [biggest  (apply max (map #(apply max %) buffer))]
    (doseq [y (range size)
            x (range size)]

      (.setColor graphics (calc-pixel-color (aget buffer y x) biggest))
      (.drawLine graphics x y x y))))

(defn draw [{buffer :buffer size :size}]
  (let [image  (BufferedImage. size size BufferedImage/TYPE_INT_RGB)
        canvas (proxy [JLabel] []
                 (paint [g] (.drawImage g image 0 0 this)))]

    (paint-canvas buffer size (.createGraphics image))

    (doto (JFrame.)
      (.add canvas)
      (.setSize (Dimension. size size))
      (.show))))

To play with the script, define a fractal 

(def fractal {:buffer (make-array Integer/TYPE 800 800) :size 800 :iteration 50})

Start calculations, 

(start fractal)

Check the result at intervals until you are satisfied. 

(draw fractal)

Below are the some shots on how the image progresses,

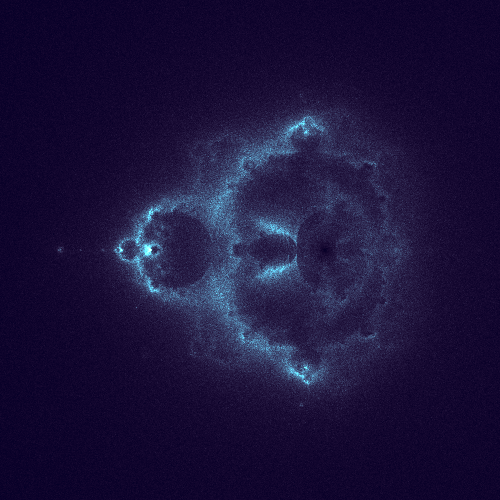
buddhabrot fractal

10 Million Points

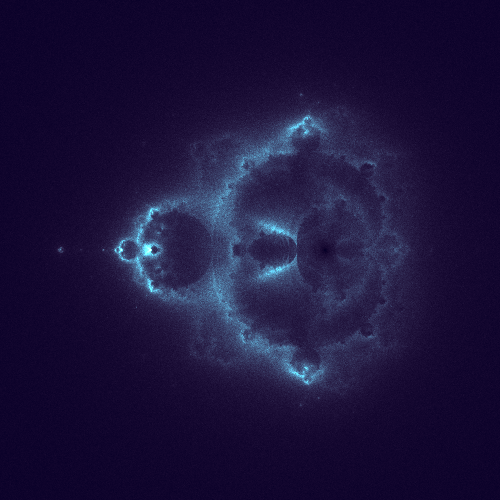
buddhabrot fractal

30 Million Points

buddhabrot fractal

60 Million Points

buddhabrot fractal

400 Million Points 400 Iterations

Tags: clojure fractal