Lindenmayer System in Clojure

An L-system or Lindenmayer system is a language, which means a set of strings that is made by the application using certain rules. L-systems can be used to generate fractals such as iterated function systems.

  • variables : F
  • constants* : + -
  • start : F
  • rules : (F -> F+F-F-F+F)

Above grammar represents the Koch curve, where F means "draw forward", + means "turn left 90",and - means "turn right 90". Following is a simple implementation in Clojure to build sentences using grammars defined like this. 

(ns lsystem
  (:use turtle))

(defn variable? [grammer symbol]
  (contains? (:variables grammer) symbol))

(defn apply-rules [grammer sentence]
  (flatten
   (map #(if (variable? grammer %) ((:rules grammer) %) %) sentence)))

(defn l-system [grammer n]
  (loop[acc n sentence (:start grammer)]
    (if (= 0 acc)
      sentence (recur (dec acc) (apply-rules grammer sentence)))))

We take the axiom (start) and apply the rules n times, with each iteration we replace the variables with their corresponding rules, so the grammar above will grow such as,

  • n=0: F
  • n=1: F+F-F-F+F
  • n=2: F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F

Grammar for the Koch curve in Clojure is represented like so, 

(def koch-curve
     {:variables #{:F}
      :constants #{:+ :-}
      :start [:F]
      :rules {:F [:F :+ :F :- :F :- :F :+ :F]}
      :actions {:F forward :+ left :- right}
      :angle 90
      :step 10})

There are some additions to the grammar, such as what actions will be mapped to the variables while drawing, angles for the turns and a step value to determine how much to move forward or backward. 

(defn draw-system [turtle grammer sentence]
  (doseq [letter sentence]
    (let [action (letter (:actions grammer))] 
      (cond
       (or (= action forward) (= action back)) 
       (action turtle (:step grammer))
       (or (= action left) (= action right)) 
       (action turtle (:angle grammer))))))

(defn setup-turtle [turtle x y]
  (pen-up turtle)
  (right turtle 90)
  (go turtle x y)
  (pen-down turtle))

After creating a sentence for the fractal all we need to do is, iterate over the letters and command turtle to do the action that is mapped to the letter. 

(def dragon-curve
     {:variables #{:X :Y}
      :constants #{:F :+ :-}
      :start [:F :X]
      :rules {:X [:X :+ :Y :F]
              :Y [:F :X :- :Y]}
      :actions {:F forward :+ left :- right}
      :angle 90
      :step 10})

(doto (turtle 450 600)
  (setup-turtle -50 -200)
  (draw-system dragon-curve (l-system dragon-curve 10))
  (show))

Lindenmayer Dragon Curve

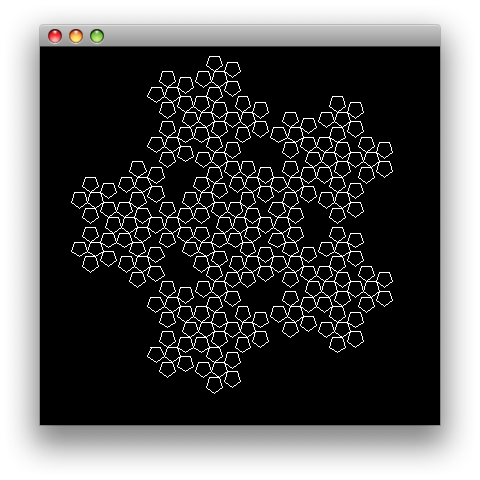
(def pentigree
     {:variables #{:F}
      :constants #{:+ :-}
      :start [:F :- :F :- :F :- :F :- :F]
      :rules {:F [:F :- :F :+ :+ :F :+ :F :- :F :- :F]}
      :actions {:F forward :+ left :- right}
      :angle 72
      :step 10})

(doto (turtle 400 400)
  (setup-turtle -90 -100)
  (draw-system pentigree (l-system pentigree 3))
  (show))

Lindenmayer System Pentigree

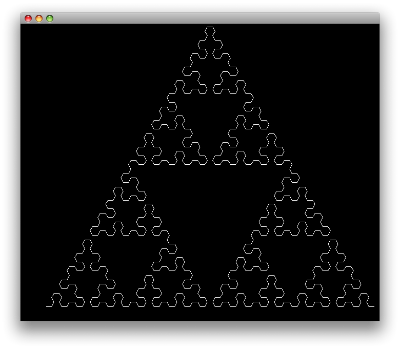
(def sierpinski-triangle
     {:variables #{:A :B}
      :constants #{:+ :-}
      :start [:A]
      :rules {:A [:B :- :A :- :B]
              :B [:A :+ :B :+ :A]}
      :actions {:A forward :B forward :+ left :- right}
      :angle 60
      :step 10})

(doto (turtle 700 600)
  (setup-turtle -300 -200)
  (draw-system sierpinski-triangle (l-system sierpinski-triangle 6))
  (show))

Lindenmayer System Sierpinski Triangle

Tags: clojure fractal