Path Finding using Rapidly-Exploring Random Tree
From Wikipedia,
A Rapidly-exploring random tree (RRT) is a data structure and algorithm designed for efficiently searching nonconvex, high-dimensional search spaces. The tree is constructed in such a way that any sample in the space is added by connecting it to the closest sample already in the tree.
(ns rrt (:refer-clojure :exclude [+ - * =]) (:use (clojure.contrib.generic [arithmetic :only [+ - *]] [comparison :only [=]])) (:use vector-2d.core) (:require kdtree))
The basic idea of the algorithm is very simple, RRT will search for a path from the start state to the goal state by expanding the search tree, algorithm is as follows,
- Initialize the tree with the starting point as root
- Pick a random point within the valid parameter space
- Search the one vertex in the tree which is nearest to the random point chosen in 2.
- Move a certain distance from this vertex in the direction of the chosen point and create there a new leaf
- Loop over step 2. to 4. while the break condition is not satisfied
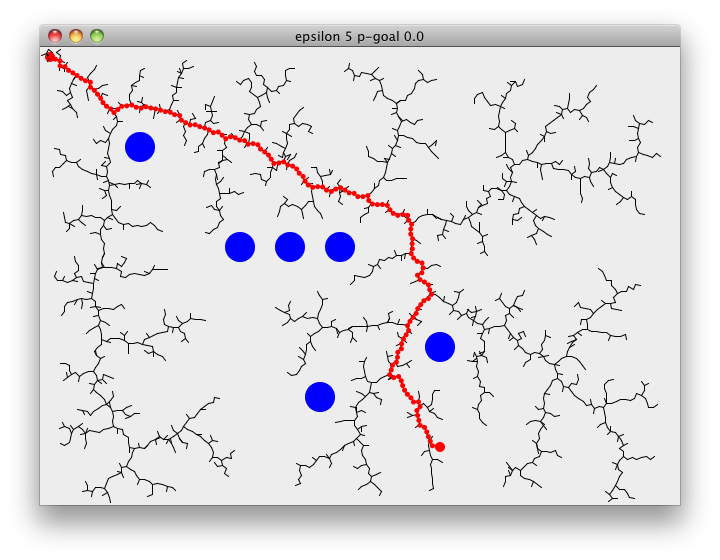
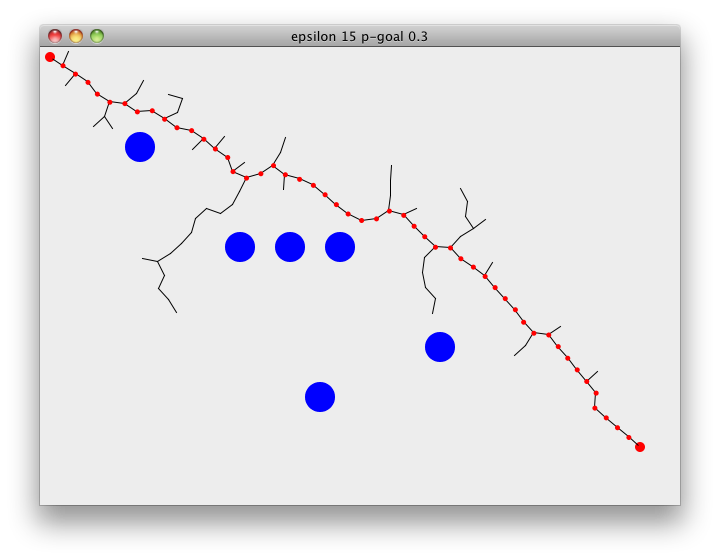
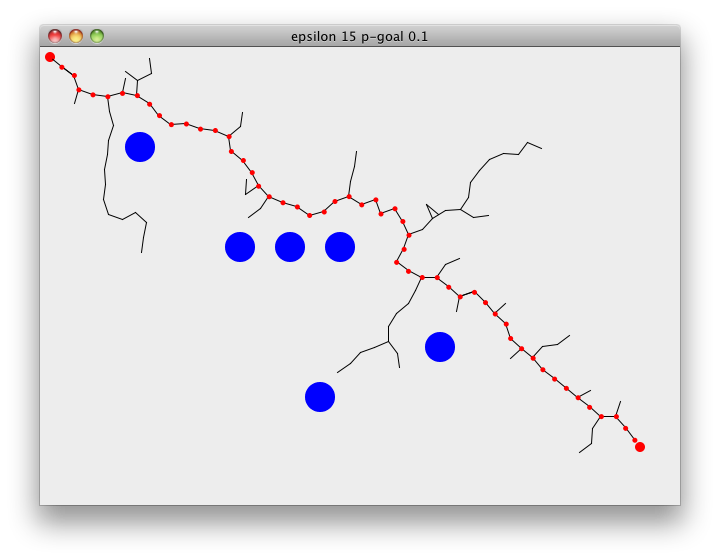
Following demonstrates RRT path finding on a 2D surface. Starting at the goal, search tree will rapidly expand through the space towards the goal. rrt-plan pretty much summarizes all of the above steps, choose-target either picks a random point on the map or returns the goal, nearest returns the closest point on the tree to the chosen target. explore then checks if we can extend the tree towards the point or not. epsilon is the distance we extend the tree by and p-goal is used to guide the search towards the goal. rrt-plan returns when we add a point to the tree that is closer than epsilon to the goal,
(defn search-world [width height & obstacles] [width height obstacles]) (defn explore [[_ _ obstacles] u v epsilon] (let [explored (+ u (to-cartesian epsilon (:t (to-polar (- v u)))))] (when-not (some true? (map #(let [[c r] %] (point-in-circle? explored c r)) obstacles)) explored))) (defn nearest [kdtree {x :x y :y}] (apply vector-2d (:point (kdtree/nearest-neighbor kdtree [x y])))) (defn choose-target [[width height] p-goal goal] (if (< 0 (rand) p-goal) goal (vector-2d (rand width) (rand height)))) (defn rrt-plan ([world start goal epsilon p-goal] (let [{:keys [x y]} start] (rrt-plan world goal epsilon p-goal {start nil} (kdtree/build-tree [[x y]])))) ([world goal epsilon p-goal tree kdtree] (let [target (choose-target world p-goal goal) nearest (nearest kdtree target)] (if (< (dist nearest goal) epsilon) (rrt-plan tree (list nearest) (tree nearest)) (if-let [explored (explore world nearest target epsilon)] (let [{:keys [x y]} explored] (recur world goal epsilon p-goal (assoc tree explored nearest) (kdtree/insert kdtree [x y]))) (recur world goal epsilon p-goal tree kdtree))))) ([tree path node] (if (nil? node) [tree path] (recur tree (conj path node) (tree node)))))
The Rapidly-exploring Random Tree algorithm is extremely simple and cheap to calculate but it is not a silver bullet, you will get a path quick but it is not guaranteed to the be the cheapest plus you will get a different path for every search.
(let [draw-circle (fn [g pt rad color] (let [[x y] (vals pt) offset (int (/ rad 2)) x (- x offset) y (- y offset)] (.setColor g color) (.fill g (java.awt.geom.Ellipse2D$Double. x y rad rad)))) draw-line (fn [g start end color] (let [[x1 y1] (vals start) [x2 y2] (vals end)] (.setColor g color) (.drawLine g x1 y1 x2 y2)))] (defn view [world start goal epsilon p-goal] (let [[width height obstacles] world [tree path iter] (time (rrt-plan world start goal epsilon p-goal))] (println iter) (doto (javax.swing.JFrame. (str "epsilon " epsilon " p-goal " p-goal)) (.add (proxy [javax.swing.JLabel] [] (paint [g] (.setRenderingHint g java.awt.RenderingHints/KEY_ANTIALIASING java.awt.RenderingHints/VALUE_ANTIALIAS_ON) (draw-circle g start 10 java.awt.Color/RED) (draw-circle g goal 10 java.awt.Color/RED) (doseq [[center radius] obstacles] (draw-circle g center radius java.awt.Color/BLUE)) (doseq [[a b] tree] (when (not (nil? b)) (draw-line g a b java.awt.Color/BLACK))) (doseq [c path] (draw-circle g c 5 java.awt.Color/RED))))) (.setSize width height) (.show)))))
Define the world,
(def w (search-world 640 480 [(vector-2d 100 100) 30] [(vector-2d 200 200) 30] [(vector-2d 300 200) 30] [(vector-2d 400 300) 30] [(vector-2d 280 350) 30] [(vector-2d 250 200) 30]))
and search,
(view w (vector-2d 10 10) (vector-2d 600 400) 15 0.3)
(view w (vector-2d 10 10) (vector-2d 600 400) 15 0.1)
(view w (vector-2d 10 10) (vector-2d 400 400) 50 0.3)

To give you an idea about its performance following table shows the average time for 1000 path finds with various epsilon and p-goal values,
core=> (print-rrt-test-table) ======================================= :epsilon | :p-goal | :time ======================================= 15 | 0.1 | 27.412393000000016 15 | 0.2 | 20.784910000000007 15 | 0.3 | 19.029839999999993 15 | 0.4 | 17.95052699999999 15 | 0.5 | 18.672436999999984 30 | 0.1 | 8.090104 30 | 0.2 | 6.6845480000000075 30 | 0.3 | 6.206767000000004 30 | 0.4 | 5.905667 30 | 0.5 | 6.293392000000007 50 | 0.1 | 3.4616730000000002 50 | 0.2 | 2.7482080000000018 50 | 0.3 | 2.4386669999999984 50 | 0.4 | 2.429180000000003 50 | 0.5 | 2.5016600000000064 =======================================
and for comparison A* search times for the same map for various grid sizes,
core=> (print-a-star-test-table) =============================== :grid-size | :time =============================== 50 | 15.309023999999988 30 | 15.811200999999986 15 | 45.569509 ===============================