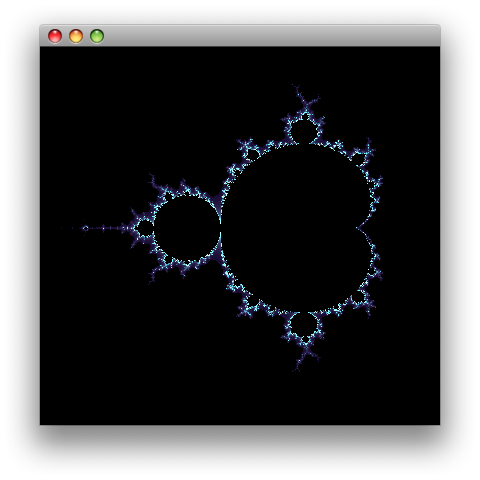
Fractals in Clojure - Mandelbrot Fractal

In this post we will cover another type of fractal called Mandelbrot. It is named after Benoit Mandelbrot. The cool thing about it is that you can zoom on it forever and at each zoom level you will get a replica of the original image. They also make great wallpapers.

The algorithm we will use goes like this,

  • We choose a rectangle in a complex plane.
  • We map our image to the complex plane we choose.
  • For each point/pixel we apply \(z = z\^2 + c\)
  • And calculate how many iterations are required for the point.
  • Paint the point according to it's iteration.

We apply \(z = z\^2 + c\) until either absolute value of the result is bigger than two or maximum iteration is reached. 

(ns mandelbrot
  (:refer-clojure :exclude [+ * <])
  (:use (clojure.contrib complex-numbers)
        (clojure.contrib.generic [arithmetic :only [+ *]]
                                 [comparison :only [<]]
                                 [math-functions :only [abs]]))
  (:import (javax.swing JFrame JLabel)
           (java.awt.image BufferedImage)
           (java.awt Dimension Color)))

(defn calc-iterations [p q max-iterations]
  (let [c (complex p q)]
    (loop [z c
           iterations 0]
      (if  (or (> (abs z) 2.0)
               (> iterations max-iterations))
        (if  ( = 0 iterations)
          0
          (- iterations 1))
        (recur (+ c (* z z)) (inc iterations))))))

For coloring the set it's up to your imagination. Set is colored using iterations, Each iteration is painted using different color. In this function, first 10 iterations are colored black to have a outer shell, last iteration is black to give inner black color, rest of the iterations are calculated using their iteration. 

(defn calc-pixel-color [iterations max-iterations]
  (if (or (< iterations 10)
          (= iterations max-iterations))
    (Color. 0 0 0)
    (let [gray (int (/ (* iterations 255) max-iterations))
          r    gray
          g    (Math/min (int ( / (* 5 ( * gray gray)) 255)) 255)
          b    (Math/min (int (+ 40 ( / (* 5 (* gray gray)) 255))) 255)]
      (Color. r g b))))

Next, we paint on the canvas. We iterate each coordinate convert it to complex plane coordinates then color it based on the iteration. 

(defn generate [x y width height max-iterations 
                graphics surface-width surface-height]
  (doseq [i (range surface-width)
          j (range surface-height)]
    (let  [p ( + x (* width (/ i surface-width)))
           q ( + y (* height (/ j surface-height)))
           iterations (calc-iterations p q max-iterations)
           color (calc-pixel-color iterations max-iterations)]
      (.setColor graphics color)
      (.drawLine graphics i j i j))))

(defn draw [x y width height iterations surface-width surface-height]
  (let [image  (BufferedImage. surface-width surface-height BufferedImage/TYPE_INT_RGB)
        canvas (proxy [JLabel] []
                 (paint [g]  
                   (.drawImage g image 0 0 this)))]

    (generate x y width height iterations 
              (.createGraphics image) surface-width surface-height)

    (doto (JFrame.)
      (.add canvas)
      (.setSize (Dimension. surface-width surface-height))
      (.show))))

We paint the resulting image on to a JLabel and put it in a JFrame. 

(draw -2.1 -1.4 3.0 3.1 32 400 400)

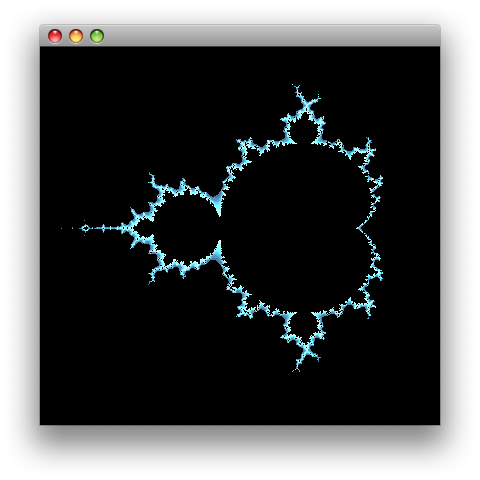
mandelbrot fractal

(draw -2.1 -1.4 3.0 3.1 100 400 400)

mandelbrot fractal

Tags: clojure fractal