Fractals in Clojure - Newton Fractal

Newton-Raphson method is a technique that is used to find the roots of a function \(f(x)\). Newton-Raphson method finds the values of the roots by approximating the root first then iterating it using the formula \(a' = a - \frac{f(a)}{f'(a)}\), with each iteration we get a more accurate root, this is done until we get a accurate enough root.

newton fractal

(ns newton.core
  (:refer-clojure :exclude [/ - + * > <])
  (:use (clojure.contrib complex-numbers)
        (clojure.contrib.generic [arithmetic :only [/ - + *]]
                                 [comparison :only [> <]]
                                 [math-functions :only [abs]])))

(defn convergence [f c step delta]
  (let [dz #(/ (- (f (+ % (complex step step))) (f %)) (complex step step))
        iter #(- % (/ (f %) (dz %)))] 
    (loop [lz c
           z (iter c)
           i 0]
      (if (or (> i 31)
              (< (abs (- z lz)) delta))
        i
        (recur z (iter z) (inc i))))))

Given a function f and a complex number c, we apply above formula, with each iteration we make better guesses using a step value, we stop either when we have tried 32 times and not find a accurate enough root, or we find an accurate enough root (a' - a will be smaller than the delta). We return the number of iterations required, that is what we use to paint the fractal. 

(defn newton [f step delta img-size complex-plane]
  (let [[width height] img-size
        [xa xb ya yb] complex-plane]
    (pmap #(let [[x y] %
                 zx (+ (/ (* x (- xb xa)) (- width 1)) xa)
                 zy (+ (/ (* y (- yb ya)) (- height 1)) ya)
                 c  (complex zx zy)]
             [x y (convergence f c step delta)]) 
          (for [y (range height) x (range width)] [x y]))))

Each pixel on our image will map to a complex number on a complex plane, first we need to calculate the complex number that corresponds to the pixel then calculate the required iterations for that pixel. When done for each pixel we get a sequence of triples representing x,y coordinates and iterations required. 

(defn draw [f step delta img-size complex-plane]
  (let [rgb #(vector (* (mod % 4) 64) (* (mod % 8) 32) (* (mod % 16) 16))
        [width height] img-size
        image (java.awt.image.BufferedImage.
               width height java.awt.image.BufferedImage/TYPE_INT_RGB)
        graphics (.createGraphics image)
        fractal (newton f step delta img-size complex-plane)]
    (doseq [point fractal]
      (let [[x y c] point
            [r g b] (rgb c)]
        (.setColor graphics (java.awt.Color. r g b))
        (.drawLine graphics x y x y)))
    (doto (javax.swing.JFrame.)
      (.add (proxy [javax.swing.JPanel] []
              (paint [g] (.drawImage g image 0 0 this))))
      (.setSize (java.awt.Dimension. width height))
      (.show))))

Drawing is done by iterating over the x,y,iteration triples and painting the pixel using a color depending on the iterations calculated (speed of convergence to a particular solution). 

(draw (fn [z] (- (* z z z) 1)) 
      0.000006 0.003 [512 512] [-1.0 1.0 -1.0 1.0])

newton fractal

(draw (fn [z] (+ (- (* z z z) (* 2 z)) 2))
      0.000006 0.003 [512 512] [-1.0 1.0 -1.0 1.0])

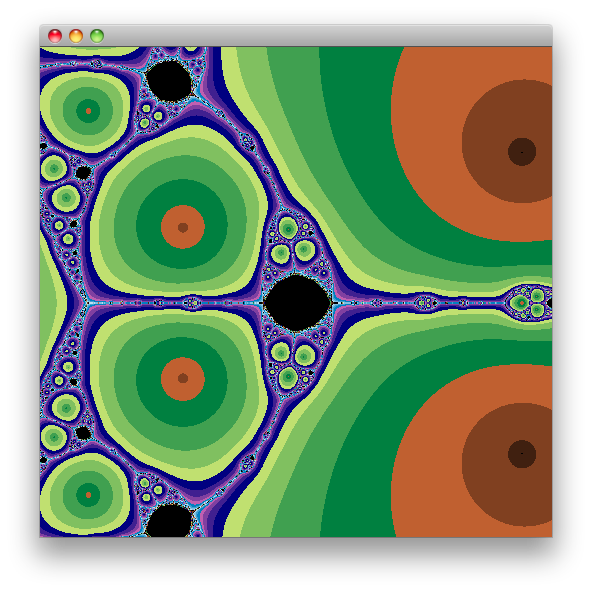
newton fractal

(draw (fn [z] 
        (complex (* (Math/sin (real z)) (Math/cosh (imag z)))
                 (* (Math/cos (real z)) (Math/sinh (imag z)))))
      0.000006 0.003 [512 512] [-2.0 2.0 -2.0 2.0])

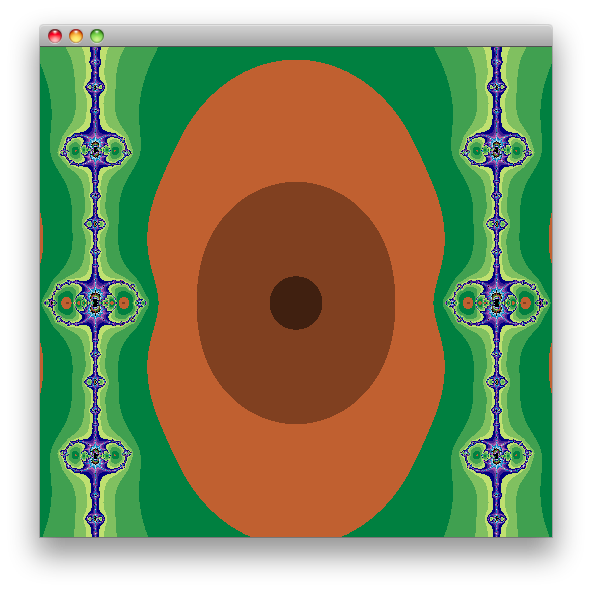
newton fractal

(draw (fn [z] (- (* z z z z) 1)) 
      0.000006 0.003 [512 512] [-1.0 1.0 -1.0 1.0])

newton fractal

Tags: clojure fractal